5.9 Geometric properties
5.9.1 Properties of a cross section
Structural Properties
- Axial Stiffness (\(E A\))
- Bending Stiffness (\(E I\))
- Torsional Stiffness (\(G J\))
Depends on shape and material!
- We have seen that there is a geometric component to stiffness
- We will examine three properties which are critical
- Cross sectional area (\(A\))
- Area moment of inertia (\(I\))
- Polar (torsional) moment of inertia (\(J\))
5.9.2 Properties of a cross section
Unlabelled Image Missing
- The area is critical in axial load because the stress is inversely proportional to the area
\[\sigma = \frac{P}{A} = \frac{P}{b \cdot h}\]
- Axial stiffness (\(EA\)) is proportional to the area
5.9.3 Properties of a cross section
Unlabelled Image Missing
- The area moment of inertia (\(I\)) goes as the third power of the thickness (about the axis of bending) \[I = \frac{b h^3}{12}\]
- The bending stiffness (\(EI\)) is directly proportional to \(I\)
- Additionally, \(h\) also critical in bending because of its relation the maximum stress
\[\sigma_{\mathrm{max}} = \frac{M h}{2 I} = \frac{6 M}{b h^2}\]
5.9.4 Properties of a cross section
Unlabelled Image Missing
Similarly, the area moment of inertia for a hollow bone is: \[I = \frac{\pi (R^4-r^4)}{4}\]
Consider an application: IM Nails

Kolossos, via Wikipedia, Creative Commons Attribution-Share Alike 3.0
5.9.5 Implications for a fracture callus
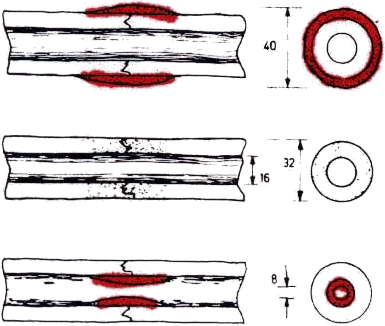
@Tencer1994
- As the callus increases the radius, the stiffness increases by \(R^4\)
- The stress (for the same load) reduces by \(\frac{1}{R^3}\)
- (These equations for circular cross sections)
5.9.6 Stiffness as a function of healing time
- Callus increases with time
- Stiffness increases with time
- Near normal stiffness at 27 days
- Does not correspond to radiographs
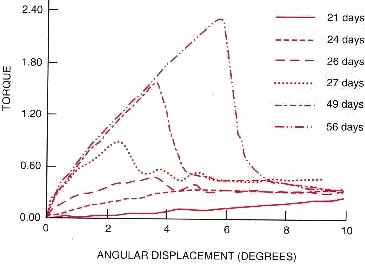
@Browner1998
5.9.7 IM Nail Diameter
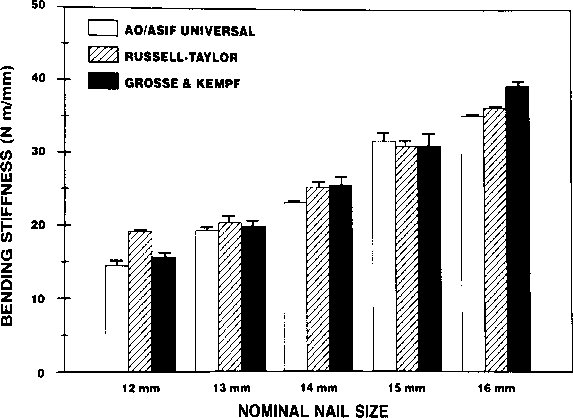
@Tencer1994
5.9.8 Slotting
- Results in more flexibility in bending and torsion
- Decreases torsional strength by significant amount
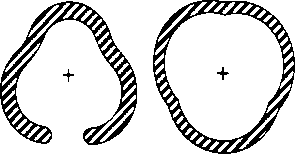

Equal values of mean width, equal thickness

Unlabelled Image Missing
\[GJ_{\mathrm{open}} = G \frac{b t^3}{3} = G \frac{\pi d t^3}{3}\] \[GJ_{\mathrm{ef}}^{\mathrm{cir}}=G \frac{\pi d^{3} t}{4}\]
Equal values of mean width, equal thickness

Unlabelled Image Missing
Assume: \[t=3 \mathrm{mm}\] \[d=25 \mathrm{mm}\]
The ratio is: \[\frac{J_{\mathrm{ef}}^{\mathrm{cir}}}{J_{\mathrm{open}}}=52\]
5.9.9 Mechanics of bone: viscoelasticity
Unlabelled Image Missing
Bone is viscoelastic: its stress-strain characteristics are dependent upon the rate of loading
Example: trabecular bone becomes stiffer in compression the faster it is loaded.
5.9.10 Credits
- @Einhorn2007
- @Le2004