| (319) |
The governing equations of electrostatics are
and
where
![]() is the electric field,
is the electric field, ![]() is the electric potential,
is the electric potential,
![]() is the electric charge density and
is the electric charge density and
![]() is the permittivity
of free space (
is the permittivity
of free space (
![]() C
C![]() Nm
Nm![]() ). The electric field
). The electric field
![]() is the force on a unit charge.
is the force on a unit charge.
In metals, it is linked to the current density
![]() by the electric conductivity
by the electric conductivity ![]() [5]:
[5]:
| (321) |
In free space, the electric field is locally orthogonal to a conducting
surface. Near the surface the size of the electric field is proportional to
the surface charge density ![]() [22]:
[22]:
Substituting Equation (319) into Equation (320) yields the governing equation
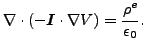 |
(323) |
Accordingly, by comparison with the heat equation, the correspondence in Table (13) arises. Notice that the electrostatics equation is a steady state equation, and there is no equivalent to the heat capacity term.
An application of electrostatics is the potential drop technique for crack
propagation measurements: a predefined current is sent through a conducting specimen. Due
to crack propagation the specimen section is reduced and its electric
resistance increases. This leads to an increase of the electric potential
across the specimen. A finite element calculation for the specimen
(electrostatic equation with ![]() ) can
determine the relationship between the potential and the crack length. This
calibration curve can be used to derive the actual crack length from
potential measurements during the test.
) can
determine the relationship between the potential and the crack length. This
calibration curve can be used to derive the actual crack length from
potential measurements during the test.
Another application is the calculation of the capacitance of a
capacitor. Assuming the space within the capacitor to be filled with air, the
electrostatic equation with ![]() applies (since there is no charge
within the capacitor). Fixing the electric potential on each side of the
capacitor (to e.g. zero and one), the electric field can be calculated by the
thermal analogy. This
field leads to a surface charge density by Equation
(322). Integrating this surface charge leads to the total
charge. The capacitance is defined as this total charge divided by the
electric potential difference (one in our equation).
applies (since there is no charge
within the capacitor). Fixing the electric potential on each side of the
capacitor (to e.g. zero and one), the electric field can be calculated by the
thermal analogy. This
field leads to a surface charge density by Equation
(322). Integrating this surface charge leads to the total
charge. The capacitance is defined as this total charge divided by the
electric potential difference (one in our equation).
For dielectric applications Equation (320) is modified into
| (324) |
where
![]() is the electric displacement and
is the electric displacement and ![]() is the free
charge density [22]. The electric displacement is coupled with the electric field
by
is the free
charge density [22]. The electric displacement is coupled with the electric field
by
| (325) |
where ![]() is the permittivity and
is the permittivity and
![]() is the relative
permittivity (usually
is the relative
permittivity (usually
![]() , e.g. for silicon
, e.g. for silicon
![]() =11.68). Now, the governing equation yields
=11.68). Now, the governing equation yields
| (326) |
and the analogy in Table (14) arises. The equivalent of Equation (322) now reads
| (327) |
The thermal equivalent of the total charge on a conductor is the total heat
flow. Notice that ![]() may be a second-order tensor for anisotropic materials.
may be a second-order tensor for anisotropic materials.