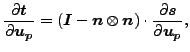Tangent contact stiffness

Due to the assumption that the projection of the slave integration point on the master surface does not change during and increment, and that the local normal on the master surface does not change either, the equations derived in the section on node-to-face contact simplity to:

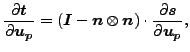$$\frac{\partial \boldsymbol{t} }{\partial \boldsymbol{u_p} } = (\b... ...ldsymbol{n}) \cdot \frac{\partial \boldsymbol{s} }{\partial \boldsymbol{u_p} },$$ (249)

where

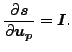$$\frac{\partial \boldsymbol{s} }{\partial \boldsymbol{u_p} }= \boldsymbol{I}.$$ (250)

Equation (223) now reduces to

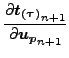$$\frac{\partial \boldsymbol{t_{(\tau)}}_{n+1} }{\partial \boldsymbol{u_p}_{n+1} } = \mu \boldsymbol{\xi }_{n+1} \otimes \left [ -\boldsymbol{n} \cd... ...c{\partial \boldsymbol{t_{(n)}}_{n+1}}{\partial \boldsymbol{u_p}_{n+1}} \right]$$

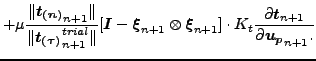$$+ \mu \frac{\Vert\boldsymbol{t_{(n)}}_{n+1} \Vert}{\Vert\boldsymb... ...ot K_t \frac{\partial \boldsymbol{t}_{n+1} }{\partial \boldsymbol{u_p}_{n+1}. }$$ (251)

Be careful to distinguish $\boldsymbol{t_{(n)}}_{n+1}$ and $\boldsymbol{t_{(\tau)}}_{n+1}$, which are tractions, from $\boldsymbol{t}_{n+1}$, which is a tangential differential displacement.