| (245) |
The traction excerted by the master face on the slave face at a slave integration point p can be written analogous to Equation (166):
| (245) |
For simplicity, in the face-to-face contact formulation it is assumed that
within an increment the location
![]() of the projection
of the slave integration points on the master face and the local Jacobian on the
master face do not change. Consequently (cf. the section 6.7.5):
of the projection
of the slave integration points on the master face and the local Jacobian on the
master face do not change. Consequently (cf. the section 6.7.5):
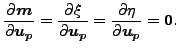 |
(246) |
and
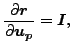 |
(247) |
which leads to
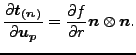 |
(248) |
This is the normal contact contribution to Equation (244).