ME5200 - Orthopaedic Biomechanics:
Lecture 4
Basic biomechanical concepts
Basic biomechanics
Forces, moments, and equilibrium
Forces
- A force is a push or a pull
- A force causes acceleration of a mass \[\begin{split}
F =& \; m a \; ( =m \ddot{x} = m \dot{v})\\
\end{split}\]
- acceleration – \(a\)
- \(a\) is also called \(\ddot{x}\) or \(\dot{v}\)
- position – \(x\)
- velocity – \(v\)
- \(\dot{()}\) the rate of change of \(()\)
- acceleration – \(a\)
- Example
- Weight – the pull of the earth’s gravity on a body
Note Mass (\(m\)) can be considered the bodies resistance to a change in its motion (ie inertia))
Moments
- Similar to a force, a moment is a
pair of forces that cause twisting \[M = I \alpha\]- the angular acceleration – \(\alpha\)
- \(\alpha\) is also called \(\ddot{\theta}\)
- \(\dot{\theta}\) – the angular velocity
- \(\theta\) – the angle (ie the current orientation)
- \(I\) is the rotational inertia
- the angular acceleration – \(\alpha\)
Notes
Moments are also called bending moments or torques
depending on the application.Moments and forces are both described as “generalized forces”
Equilibrium
We have already used another important concept, equilibrium
Forces and changes in momentum remain in balance \[\begin{split} \displaystyle\sum F =& \; m a \\ \displaystyle\sum M =& \; I \alpha \\ \end{split}\]
Much of biomechanics boils down to applying these equations
Static equilibrium – the balance of forces that occurs
when there is no acceleration \[\begin{split} \sum F =& \; 0 \\ \sum M =& \; 0 \\ \end{split}\]
“Mathematical tools” in biomechanics
Vectors and scalars
Vectors
Vectors are quantities that have an associated magnitude and direction.\(^{**}\)
Vector have components
- \(\vec{F}_x = {F}_x i\)
- \(\vec{F}_y = {F}_y j\)
- \(\vec{F} = \vec{F}_x + \vec{F}_y = {F}_x i +{F}_y j\)
Examples of vectors
- Forces (Weight)
- Moments (Torques)
- Velocities
Vector sums
- Vector addition is component by component
- Proper (2D) summation results in a parallelogram
Scalars
- Scalars have magnitude without direction.
- Examples
- Levels of gray in a image
- Patient mass
- Patient bone density
- Concentration of a drug per unit volume
- Time
- Altitude
Relationship between vectors and scalars
- Scalars and vectors can be linked mathematically

Example: diffusion of nutrients into intervertebral disk driven by gradient of glucose
Gradient of a scalar
\[\nabla f = \left(\frac{\partial f}{\partial x_1 }, \dots, \frac{\partial f}{\partial x_n } \right).\]
Gradient of a vector becomes a 2nd rank tensor \[\mathbf{f}=({{f}_{1}},{{f}_{2}},{{f}_{3}})\] \[\nabla \mathbf{f}=\frac{\partial {{f}_{j}}}{\partial {{x}_{i}}}{{\mathbf{e}}_{i}}{{\mathbf{e}}_{j}}\]
Example: strain is gradient of displacement vector
- \[\vec{u} = u {{e_x}}+ v {{e_y}}+ w {{e_z}}\]
- \[= {\varepsilon_{ij}}= \nabla \vec{u} = \left[ \begin{array}{ccc} {\varepsilon_{xx}}& {\varepsilon_{xy}}& {\varepsilon_{xz}}\\ {\varepsilon_{yx}}& {\varepsilon_{yy}}& {\varepsilon_{yz}}\\ {\varepsilon_{zx}}& {\varepsilon_{yz}}& {\varepsilon_{zz}}\\ \end{array} \right]\]
Divergence
Similarly, the divergence operator (\(\nabla \cdot ()\)) reduces the
rank of a tensor- i.e., makes a scalar out of a vector
Example: the divergence calculates the strength
of a source or sink of a velocity field in fluid flow
Rigid body and flexible body assumptions
- All bodies are flexible, meaning, all bodies deform when loaded
- For convenience, we often assume that a body is rigid
- (ie we assume that it does not deform when loaded.)
- With this assumption, the mechanics/mathematics is simplified
Review of Stress and strain
Normal stress
- Normal stress is the resultant normal force over a given area
\[\sigma = \frac{P}{A}\]
Shear stress
- Shear stress is the resultant shear force over a given area
\[\tau = \frac{V}{A}\]
Stresses on arbitrary planes
- Since different “cuts” must yield the same resultant force, the stress depends on your plane of observation
- Each type of stress is simultaneously present1
- A body can fail in shear even when loaded by normal stress
- Ductile materials typically yield due to shear stress
- Brittle materials typically crack due to normal stress
Stress
Note
- Stresses result from equilibrium (ie the sum of forces)
- It is possible to have stress without strain
- Example: thermal expansion/contraction
- Exothermic reactions such as bone cement
- Cement then adjusts to body temperature
- Constrained by bone and implant \(\rightarrow\) stress
- Example: thermal expansion/contraction
Strain
Normal strain
- Normal strain is the change in length over the original length
\[{\varepsilon}= \frac{\Delta l}{l}\]
Shear strain
- Shear strain (\(\gamma\)) is proportional to the shear angle (\(\alpha\)) \[\gamma = \alpha\]
Strain
Note
- Strain is defined by deformation
- It is possible to have strain without stress
- Tissues expand with moisture content
- PMMA shrinkage during polymerization
A chain of relationships in biomechanics
| Constraints |
| \(\Updownarrow\) |
| Deformation |
| \(\Updownarrow\) |
| Strain |
| \(\Updownarrow\) |
| Stress |
| \(\Updownarrow\) |
| Equilibrium |
| \(\Updownarrow\) |
| Applied Loads |
- Each arrow represents a relationship that must be understood and properly accounted
Deformation and stiffness
Skeletal structures and types of load
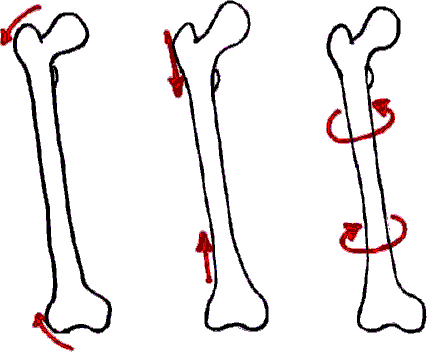
- Bending
- Axial Loading
- Tension
- Compression
- Torsion
Stiffness
- Stiffness is a structural relationship between deflection and load
- The slope of the load-deflection curve (\(k\)) is the structural stiffness
- Two factors influence the stiffness
- Material response
- Geometry
Structural properties
Material Properties
- Elastic modulus (\(E\) and \(G\))
- Yield stress (\(\sigma_Y\))
- Toughness (brittle/ductile) (\(K\))
Independent of shape!
Geometric Properties
- Material distribution
- Cross sectional area (\(A\))
- Area moment of inertia (\(I\))
- Polar moment of inertia (\(J\))
Independent of material!
Structural Properties
- Axial Stiffness (\(E A\))
- Bending Stiffness (\(E I\))
- Torsional Stiffness (\(G J\))
Depends on shape and material!
Material properties
Stress \(\Longleftrightarrow\) Strain
\(E\) – the elastic modulus
- The elastic modulus is the most critical material property
- Strain \(\varepsilon = \frac{\Delta l}{l}\)
- Stress \(\sigma = \frac{P}{A}\)
- Slope – \(E\)
Stress \(\Longleftrightarrow\) Strain
- Moduli for common materials (GPa)
| Material | Modulus |
|---|---|
| Stainless Steel | 200 |
| Titanium | 110 |
| Cortical Bone | 7-21 |
| Bone Cement | 2.5-3.5 |
| Cancellous Bone | 0.7-4.9 |
| UHMW-PE | 1.4-4.2 |
Energy and its relation to material response
Elastic-plastic behavior
- Initial loading is “elastic” (no permanent deformation)
- unloads back to origin
- Elastic energy is stored in the material
- it can be recovered (like a spring)
- \(U=\frac{1}{2} \sigma \varepsilon = \frac{1}{2} E \varepsilon^2\)
- it can be recovered (like a spring)
Elastic-plastic behavior
- Loading past yield (\(\sigma_Y\)) causes permanent set
- Typical unload follows the slope of the elastic region
- Energy is dissipated as plastic work (\(W_P\))
- Loading to the ultimate tensile strength (\(\sigma_{UTS}\)) causes failure and additional energy dissipation (\(W_F\))
Bone density and the elastic modulus
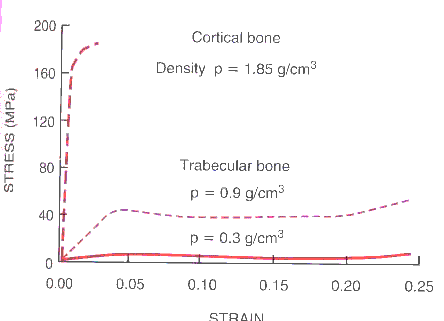
- Bone density a strong effect on modulus and other properties
- Subtle changes greatly changes strength and elastic modulus
- Density changes from:
- normal aging
- disease
- malnutrition
- use
- disuse
- …
Energy and energy dissipation
- In orthopaedics, two kinds of energy are of great concern:
- kinetic and potential
- Kinetic energy is the energy of a particle in motion
\[K = \frac{1}{2} m V^2\]
- Examples: gun shot impact, motor vehicle crash
- Potential energy is the energy associated with a fall from
a height \[U = m g h\]
- During the fall, all potential energy is converted to kinetic energy just before impact
- There are other relevant forms of potential energy
Energy and energy dissipation
- Energy is “conserved”, all energy in the system goes to something
- If enough energy is available, some goes to permanent deformation of the “structure” (bones, soft tissue, implants, etc)
Toughness: brittle vs ductile
- The fracture toughness is a measure of energy required to propagate a crack through a material
- Brittle materials have low toughness, not much energy is required
- Ductile materials have high toughness, much energy is required
Strength vs toughness
- Strength (\(\sigma_{UTS}\)) is a measure of how much stress a material can carry
- Toughness is a measure of energy dissipated during failure (crack propagation)
Strength vs fatigue strength
- Cyclic loading (repetitive load and unload) can cause “fatigue failures” at loads much lower than the ultimate tensile strength
- The S-N curve – plot of load vs number of cycles to failure
- Some materials exhibit a fatigue strength (\(\sigma_f\))
- The curve levels off and the material has infinite fatigue life below that stress
Properties of bone
Mechanics of bone: anisotropy
- Isotropy –
- Most metals – stainless, titanium, cobalt chrome
- Anisotropy –
- Strength and modulus both depend on direction
- Bone is weakest in shear, then tension, then compression.
| Compression | \(< 212\) N/m\(^2\) |
| Tension | \(< 146\) N/m\(^2\) |
| Shear | \(< 82\) N/m\(^2\) |
Types of bone fracture
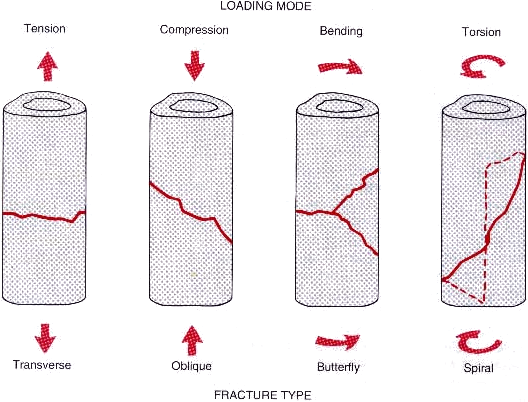
Types of bone fracture
Axial load

- In tension, failure occurs due to normal stress
- In compression, failure occurs on the plane where shear is maximized
Types of bone fracture
Bending load
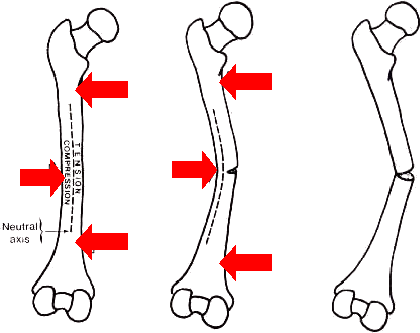

- Compression strength is greater than tensile strength
- Fails in tension, possibly with a butterfly fragment
Types of bone fracture
Bending and compression load
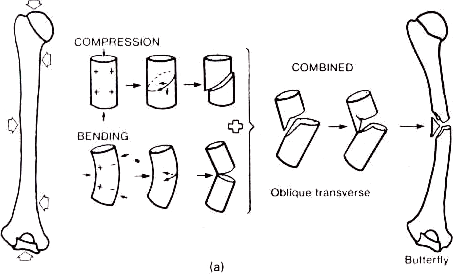
- Combined compression and bending leads to oblique fracture with butterfly fragment
Types of bone fracture
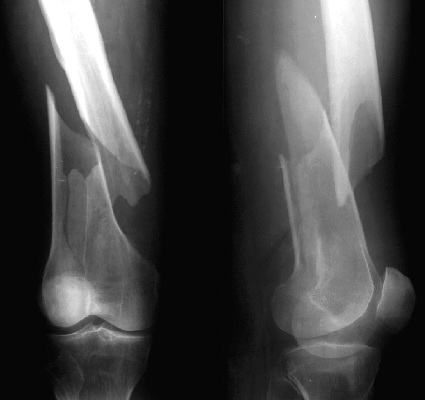
Torsion
- Like stress, components of strain depend on direction of observation
- When torsion applied, tension occurs on a diagonal
- Fractures propagate perpendicular to this tension diagonal
- Spiral fracture 45\(^o\) to the long axis
Geometric properties
Properties of a cross section
Structural Properties
- Axial Stiffness (\(E A\))
- Bending Stiffness (\(E I\))
- Torsional Stiffness (\(G J\))
Depends on shape and material!
- We have seen that there is a geometric component to stiffness
- We will examine three properties which are critical
- Cross sectional area (\(A\))
- Area moment of inertia (\(I\))
- Polar (torsional) moment of inertia (\(J\))
Properties of a cross section
- The area is critical in axial load because the stress is inversely proportional to the area
\[\sigma = \frac{P}{A} = \frac{P}{b \cdot h}\]
- Axial stiffness (\(EA\)) is proportional to the area
Properties of a cross section
- The area moment of inertia (\(I\)) goes as the third power of the thickness (about the axis of bending) \[I = \frac{b h^3}{12}\]
- The bending stiffness (\(EI\)) is directly proportional to \(I\)
- Additionally, \(h\) also critical in bending because of its relation the maximum stress
\[\sigma_{\mathrm{max}} = \frac{M h}{2 I} = \frac{6 M}{b h^2}\]
Properties of a cross section
Similarly, the area moment of inertia for a hollow bone is: \[I = \frac{\pi (R^4-r^4)}{4}\]
Consider an application: IM Nails

Implications for a fracture callus
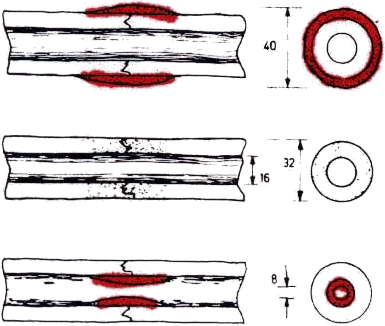
- As the callus increases the radius, the stiffness increases by \(R^4\)
- The stress (for the same load) reduces by \(\frac{1}{R^3}\)
- (These equations for circular cross sections)
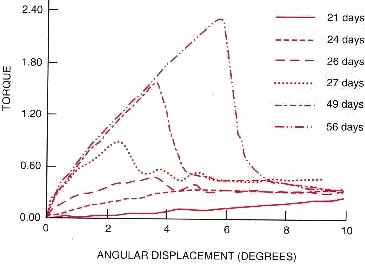
Stiffness as a function of healing time
- Callus increases with time
- Stiffness increases with time
- Near normal stiffness at 27 days
- Does not correspond to radiographs
IM Nail Diameter
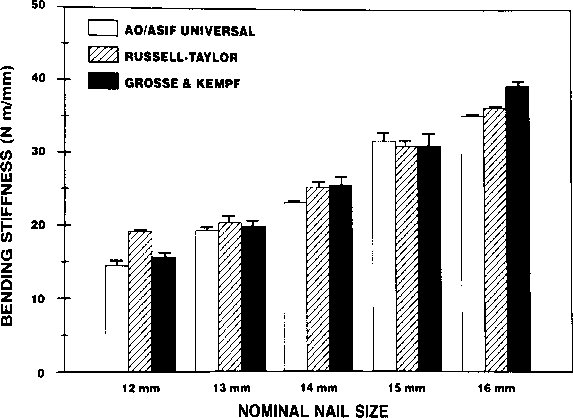
Slotting
- Results in more flexibility in bending and torsion
- Decreases torsional strength by significant amount
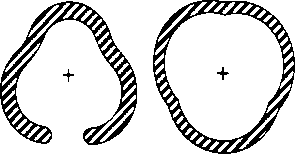

Equal values of mean width, equal thickness
\[GJ_{\mathrm{open}} = G \frac{b t^3}{3} = G \frac{\pi d t^3}{3}\] \[GJ_{\mathrm{ef}}^{\mathrm{cir}}=G \frac{\pi d^{3} t}{4}\]
Equal values of mean width, equal thickness
Assume: \[t=3 \mathrm{mm}\] \[d=25 \mathrm{mm}\]
The ratio is: \[\frac{J_{\mathrm{ef}}^{\mathrm{cir}}}{J_{\mathrm{open}}}=52\]
Mechanics of bone: viscoelasticity
Bone is viscoelastic: its stress-strain characteristics are dependent upon the rate of loading
Example: trabecular bone becomes stiffer in compression the faster it is loaded.
Credits
- @Einhorn2007
- @Le2004
except in unusual circumstances↩︎