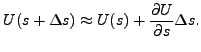Postprocessing the sensitivity

Postprocessing is only done for geometrical design variables. The postprocessing procedure is coded in sensitivity.c and consists of the following steps:

• Changing from a shape function smeared sensitivity representation to local sensitivities.
• For quadratic elements: interpolating the sensitivities at the middle nodes to the vertex nodes
• Filtering the sensitivities
• Creating a transition region from the design node region to its complement
• Modifying the sensitivities due to constraint conditions

Now the steps are treated in more detail:

• The sensitivity for geometric design variables is calculated by moving each design variable an infinitesimal distance in a direction normal to the external surface. Through the shape functions this motion extends across an area consisting of all external faces to which the design node belongs. The sensitivity is localized through division by the integral of the shape functions taking the value 1 at the node at stake (distributesens.f).
• For quadratic faces frequently a checkerboard pattern arises for the sensitivities. For this type of elements it has proven advantageous to disregard the sensitivities calculated at the vertex nodes. They are replaced by an interpolation of the values at the midnodes of all external design faces (quadraticsens.f).
• Filtering the sensitivities boils down to a local smoothing. The sensitivity values at a given node are thereby replaced by a weighted sum of the sensitivities of the nodes within a sphere with a user-defined radius. The weighting function is 1 at the node at stake and decreases radially in a user-defined way to zero at the edge of the sphere. The available filter functions are linear, quadratic and cubic. If the parameter DIRECTION WEIGHTING is active on the *FILTER card the sensitivity values at a node i are replaced by a weighted sum of the sensitivities at the nodes j within the sphere multiplied by the scalar product of the normal vector at j and the normal vector at i.
• If the parameter BOUNDARY WEIGHTING=YES is selected on the *FILTER card the sensitities are linearly decreased to zero at the edge of the design domain. This edge is defined by all nodes which are not design variables but belong to external faces which contain at least one design variable. If a design node lies within a user-defined boundary weighting distance from this edge a linear reduction proportional to the actual distance is applied. This assures a smooth transition of the sensitivities to zero at the edge of the design domain.
• Constraints are taken into account by projecting the unconstrained sensitivities on the complement of the subspace consisting of the active constraints. Suppose the domain is n-dimensional (n design variables) and the subspace has the dimension m (m constraints). Then the sensitivities of the constraints can be arranged as basis vectors in a nxm matrix. The projection p of a vector b on the subspace satisfies the orthogonality condition:

  $$N^T (b-p)=0.$$ (552)

  
  

  Since p belongs to the subspace it can be written as a linear combination of the basis vectors $p=Nx$, where $x$ is a mx1 vector of coefficients. Consequently:

  $$N^T N x = N^T b,$$ (553)

  
  

  from which x can be solved yielding:

  $$p=N(N^T N)^{-1} N^T b.$$ (554)

  
  

  The complement of the projection vector is $I-N(N^T N)^{-1} N^T$. Denoting $A=(N^T N)^{-1}$, the constrained sensitivies $c$ are obtained from the unconstrained sensitivities $b$ by:

  $$c=(I-NAN^T) b,$$ (555)

  
  

  or, in component notation:

  $$c_i=b_i-\sum_k w_{ik},$$ (556)

  
  

  where

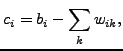  $$w_{ik}=\left( \sum_j N_{ij} A_{j \underline{k}} \right) \left( \sum_l (N^T)_{\underline{k}l} b_l \right)$$ (557)

  
  

  (no summation over k in the last equation).

  Active constraints are constraints which

  • are fulfulled AND
  • for which the Lagrange multiplier points to the non-feasible part of the space

  To this end the algorithm starts with all constraints which are fulfilled an removes the constraints one-by-one for which the Lagrange multiplier points to the feasible part of the space.