Stationary laminar viscous compressible airfoil flow

Figure 38: Pressure coefficient for laminar viscous flow about a naca012 airfoil

Figure 39: Friction coefficient for laminar viscous flow about a naca012 airfoil

A further example is the laminar viscous compressible flow about a naca012 airfoil. Results for this problem were reported by [55]. The entrance Mach number is 0.85, the Reynolds number is 2000. Of interest is the steady state solution. In CalculiX this is obtained by performing a transient CFD-calculation up to steady state. The input deck for this example is called naca012_visc_mach0.85_veryfine.inp and can be found amoung the CFD test examples. Basing the Reynolds number on the unity chord length of the airfoil, an entrance unity velocity and a entrance unity density leads to a dynamic viscosity of $\mu=5 \times 10^{-4}$. Taking $c_p=1$ and $\kappa=1.4$ leads to a specific gas constant $r=0.2857$ (all in consistent units). Use of the entrance Mach number determines the entrance static temperature to be $T_s=3.46$. Finally, the ideal gas law leads to a entrance static pressure of $p_s=0.989$. Taking the Prandl number to be one determines the heat conductivity $\lambda=5 \time 10^{-4}$. The surface of the airfoil is assumed to be adiabatic.

The results for the pressure and the friction coefficient at the surface of the airfoil are shown in Figures 38 and 39, respecively, as a function of the shock smoothing coefficient. The pressure coefficient is defined by $c_p=(p-p_\infty)/(0.5 \rho_\infty v_\infty^2)$, where p is the local static pressure, $p_\infty$, $\rho_\infty$ and $v_\infty$ are the static pressure, density and velocity at the entrance, respectively. The friction coefficient is defined by $\tau_w/(0.5 \rho_\infty v_\infty^2)$, where $\tau_w$ is the local shear stress. Both graphs agree quite well with the literature, especially if one takes into account that the sources cited by Mittal also vary. Notice that the mesh at the airfoil is very fine. Indeed, $y^+$ at the boundary of the first layer of elements adjacent to the airfoil, defined by

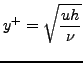$$y^+=\sqrt{\frac{u h}{\nu}}$$ (2)

where u is the velocity in x-direction at that position, h is the element height and $\nu$ is the kinematic viscosity, reaches the value of 0.2. In general,no value exceeding 1 is recommended.