 |
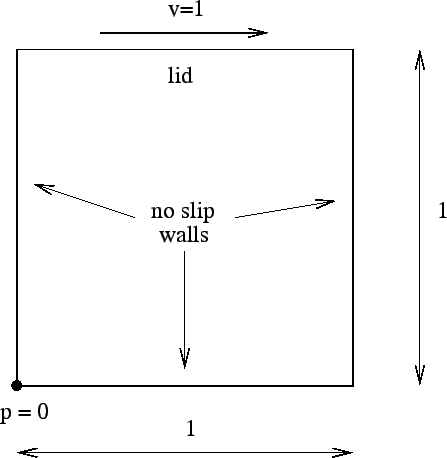
The lid-driven cavity is a well-known benchmark problem for viscous incompressible fluid flow [85]. The geometry at stake is shown in Figure 26. We are dealing with a square cavity consisting of three rigid walls with no-slip conditions and a lid moving with a tangential unit velocity. We are interested in the velocity and pressure distribution for a Reynolds number of 400.
The input deck looks like (this deck is also available in the cfd test suite as file lid400.inp):
**
** Structure: lid-driven cavity
** Test objective: incompressible, viscous, laminar, 3D fluid
**
*NODE, NSET=Nall
1,5.000000000000e-01,5.000000000000e-01,0.0
...
*ELEMENT, TYPE=F3D8, ELSET=Eall
1, 1, 2, 3, 4, 5, 6, 7, 8
...
*SURFACE, NAME=SOLIDSURFACE
40, S2
...
*MATERIAL,NAME=WATER
*DENSITY
1.
*FLUID CONSTANTS
1.,.25E-2,293.
*SOLID SECTION,ELSET=Eall,MATERIAL=WATER
*INITIAL CONDITIONS,TYPE=FLUID VELOCITY
Nall,1,0.
Nall,2,0.
Nall,3,0.
*INITIAL CONDITIONS,TYPE=PRESSURE
Nall,1.
**
*STEP,INCF=5000
*STATIC
*BOUNDARYF
** BOUNDARYF based on fixz
1, S3, 3,, 0.000000
...
** BOUNDARYF based on in
1601, S1, 1,, 0.000000
...
** BOUNDARYF based on in
1601, S1, 2,, 1.000000
...
** BOUNDARYF based on in
1601, S1, 3,, 0.000000
...
** BOUNDARYF based on wall
40, S2, 1,, 0.000000
...
** BOUNDARYF based on wall
40, S2, 2,, 0.000000
...
** BOUNDARYF based on wall
40, S2, 3,, 0.000000
...
*BOUNDARYF
1600, S3, 8,8, 1.000000
*NODE FILE,FREQUENCYF=5000
VF,PSF
*END STEP
Although the problem is essentially 2-dimensional it was modeled as a 3-dimensional problem with unit thickness since 2-dimensional fluid capabilities are not available in CalculiX. The mesh (2D projection) is shown in Figure 27. It consists of 8-node brick elements. There is one element layer across the thickness. This is sufficient, since the results do not vary in thickness direction. The input deck starts with the coordinates of the nodes and the topology of the elements. The element type for fluid volumetric elements is the same as for structural elements with the C replaced by F (fluid): F3D6. The faces belonging to solid surfaces are listed next. A face is characterized by an element number and an internal face number. Solid surfaces are surfaces at which the fluid adheres, i.e. in the presence of viscosity the velocity vector adjacent to a solid surface is the same as the velocity of the surface itself. All solid surfaces must be collected into a SURFACE definition with the name SOLIDSURFACE (no upper case required, though).
The material definition consists of the density, the heat capacity and the dynamic viscosity. The density is set to 1. The heat capacity and the dynamic viscosity are entered underneath the *FLUID CONSTANTS keyword. The heat capacity is not needed since the calculation is steady state, so its value here is irrelevant. The value of the dynamic viscosity was chosen such that the Reynolds number is 400. The Reynolds number is defined as velocity times length divided by the kinematic viscosity. The velocity of the lid is 1, its length is 1 and since the density is 1 the kinematic and dynamic viscosity coincide. Consequently, the kinematic viscosity takes the value 1/400. The material is assigned to the elements by means of the *SOLID SECTION card.
The unknowns of the problem are the velocity and static pressure. No thermal boundary conditions are provided, so the temperature is irrelevant. All initial values for the velocity and pressure are set by means of the *INITIAL CONDITIONS,TYPE=FLUID VELOCITY and *INITIAL CONDITIONS,TYPE=PRESSURE cards. Notice that for the velocity the initial conditions have to be specified for each degree of freedom separately.
The step is as usual started with the *STEP keyword. The maximum number of increments, however, is for fluid calculations governed by the parameter INCF. For steady state calculations the keyword *STATIC is to be used. If there are no time increment values beneath this line the increment size is automatically chosen such that the procedure is stable. The boundary conditions for fluid calculations are defined on the faces and are prescribed using the *BOUNDARYF card. Recall that non-homogeneous (i.e. nonzero) boundary conditions have to be defined within a step, homogeneous ones may be defined before or within the step. Here, all boundary conditions have been defined within the step. They include zero velocity at the fixed walls, a velocity of 1 in the y-direction on the lid, and zero velocity in z-direction on the side walls. The pressure has been set to 1 on face 3 of element 1600. In CFD pressure boundary conditions can only be set on faces for which not all velocity components are prescribed. Consequently, in the present example, the pressure could not have been set on faces belonging to the walls and the lid.
The step ends with a nodal print request for the velocity VF and the static pressure PSF. The printing frequency is defined to be 5000 by means of the FREQUENCYF parameter. This means, that results will be stored every 5000 increments.
The velocity distribution in y-direction (i.e. the direction tangential to the lid) is shown in Figure 28. The smallest value (-0.33) and its location agree very well with the results in [85]. Figure 29 shows a vector plot of the velocity. Near the lid there is a large gradient, in the lower left and lower right corner are dead zones. The pressure plot (Figure 30) reveals a low pressure zone in the center of the major vortex and in the left upper corner. The right upper corner is a stagnation point for the y-component of the velocity and is characterized by a significant pressure built-up.